샘플 데이터 베이스 구조

기본 용어 정리

JOIN : ▷◁
※ 세타 조인
정의
R(X), S(Y), A∈X, B∈Y 에 대하여
-> 릴레이션 R과 릴레이션 S의 애트리뷰트 X, Y
-> A는 X에 포함된 애트리뷰트, B는 Y에 포함된 애트리뷰트
-> 릴레이션 ≒ 테이블, 애트리뷰트 ≒ 컬럼(속성)
R ▷◁AθB S = { r · s | r∈R ∧ s∈S ∧ ( r.Aθs.B) }
-> A, B : 조인 애트리뷰트(join attribute) -> 조인의 기준의 되는 공통 속성
-> 릴레이션 R과 S를 조인하는 데, R의 속성 A와 S의 속성 B를 기준으로 하여 R과 S의 부분집합을 떼어서 합친다.
-> 릴레이션의 결과 차수 -> R의 차수 + S의 차수 ;; 차수 : 컬럼의 개수
-> 결과 릴레이션의 애트리뷰트는 원 소속 릴레이션 이름을 애트리뷰트 앞에 한정어 (= alias. HR.~ ... )로 붙여 일관성을 유지
- 이 연산의 결과 릴레이션이 갖는 애트리뷰트는
- 학생.학번, 학생.이름, 학생.학년, 학생.학과, 등록.과목번호, 등록.성적, 등록.중간성적, 등록.기말성적으로 표현
- 그러나 상이한 애트리뷰트는 보통 그 이름만 사용. 필드의 이름이 동일한 경우에만 한정어를 사용한다.
### θ(=비교 연산자)의 종류 : =, ≠, <, ≤, >,≥
※ 동일 조인
정의
세타 조인에서 θ가 "="인 경우
R▷◁A=BS = { r·s | r∈R ∧ s∈S ∧ ( r.A=s.B )
예)
select
*
from STUDENT s
join ENROL e
on s.Sno = e.Sno;| 학생.학번 | 이름 | 학년 | 학과 | 등록.학번 | 과목번호 | 성적 | 중간성적 | 기말성적 |
| 100 | 나수영 | 4 | 컴퓨터 | 100 | C413 | A | 90 | 95 |
| 100 | 나수영 | 4 | 컴퓨터 | 100 | E412 | A | 95 | 95 |
| 200 | 이찬수 | 3 | 전기전자 | 200 | C123 | B | 85 | 80 |
| 300 | 정기태 | 1 | 컴퓨터 | 300 | C312 | A | 90 | 95 |
| 300 | 정기태 | 1 | 컴퓨터 | 300 | C324 | C | 75 | 75 |
| 300 | 정기태 | 1 | 컴퓨터 | 300 | C413 | A | 95 | 90 |
| 400 | 송병길 | 4 | 컴퓨터 | 400 | C312 | A | 90 | 95 |
| 400 | 송병길 | 4 | 컴퓨터 | 400 | C324 | A | 95 | 90 |
| 400 | 송병길 | 4 | 컴퓨터 | 400 | C413 | B | 80 | 85 |
| 400 | 송병길 | 4 | 컴퓨터 | 400 | E412 | C | 65 | 75 |
| 500 | 박종화 | 2 | 산업공학 | 500 | C312 | B | 85 | 80 |
※ 자연 조인(Natural Join : ▷◁n)
R(X), S(Y)의 조인 애트리뷰트를 Z(=X∩Y)라 하면
-> 조인 속성 : 조인 조건
R▷◁nS
= {<r · s>[X∪Y] | r∈R∧s∈S∧r[Z]=s[Z] }
-> 속성 X와 Y의 합집합으로 이루어진 튜플들의 조건은 r은 R의, s는 S의 튜플이면서, r의 조인 조건 = s의 조인 조건을 만족하는 튜플들이 자연 조인의 결과이다.
= πX∪Y(sZ=Z(R×S))
- 카티션 프로덕트 ( X ) -> 릴레이션 R과 S를 조건 없이 그냥 합쳐서 붙여 놓은 것
- 카티션 곱, Cross Join 조인 조건절을 적지 않게 되면 해당 테이블에 대한 모든 데이터를 전부 가져오는 현상 이를 카티션 곱이라고 부른다.
- 셀렉트(s) : 일반 where 조건 -> 수평적 분할 -> 일반 릴레이션에서 특정 row를 가져 오는 연산
- 예를 들어 select * from table where id = 1이라는 sql이 있다면 id가 1인 로우가 조회되는데 이러한 수평적인 연산이 실렉트 연산
- 프로젝트(ㅠ) : 반대로 수직적인 분할 -> 실제 sql로는 조회할 수 없는 논리적인 연산이라고 생각하자.
- 쉽게 말해 테이블의 구조에서 하나 이상의 열(column)을 잘라서 가져오는 연산이다.
- 위의 식을 이해해보면서 자연 조인의 로직을 이해해보자.
- 릴레이션 R과 S를 Cross Join한 결과 중에서 위에서 정의한 조인 속성(Z(=X∩Y))을 만족하는 행을 수평 단위로 셀렉트한다.
- 해당 결과에서 속성 X와 Y의 합집합에 해당하는 컬럼을 수직적으로 분할한 결과가 자연 조인의 결과이다.
= ㅠX∪Y(R▷◁Z=ZS)
-- 즉 동일 조인의 결과에서 중복되는 애트리뷰트를 제거
예)
select
*
from STUDENT s
natural join ENROL e
where s.Sno = e.Sno;| 학번 | 이름 | 학년 | 학과 | 과목번호 | 성적 | 중간성적 | 기말성적 |
| 100 | 나수영 | 4 | 컴퓨터 | C413 | A | 90 | 95 |
| 100 | 나수영 | 4 | 컴퓨터 | E412 | A | 95 | 95 |
| 200 | 이찬수 | 3 | 전기전자 | C123 | B | 85 | 80 |
| 300 | 정기태 | 1 | 컴퓨터 | C312 | A | 90 | 95 |
| 300 | 정기태 | 1 | 컴퓨터 | C324 | C | 75 | 75 |
| 300 | 정기태 | 1 | 컴퓨터 | C413 | A | 95 | 90 |
| 400 | 송병길 | 4 | 컴퓨터 | C312 | A | 90 | 95 |
| 400 | 송병길 | 4 | 컴퓨터 | C324 | A | 95 | 90 |
| 400 | 송병길 | 4 | 컴퓨터 | C413 | B | 80 | 85 |
| 400 | 송병길 | 4 | 컴퓨터 | E412 | C | 65 | 75 |
| 500 | 박종화 | 2 | 산업공학 | C312 | B | 85 | 80 |
동일 조인과는 다르게 '학번' 속성이 한정어를 사용하지 않고 한 번만 나오는 것을 알 수 있다.
※ 세미 조인
애트리뷰트를 Z(=X∩Y)라 하면
R▷< S = R▷◁n(ㅠZ(S)) = ㅠX(R▷◁nS)
-> 릴레이션 S에 대해서 R과 S에 모두 속한 속성을 뽑아 새로운 릴레이션을 만들고, 새로 만든 릴레이션과 R을 자연 조인하면 세미 조인의 결과를 볼 수 있다.
예)

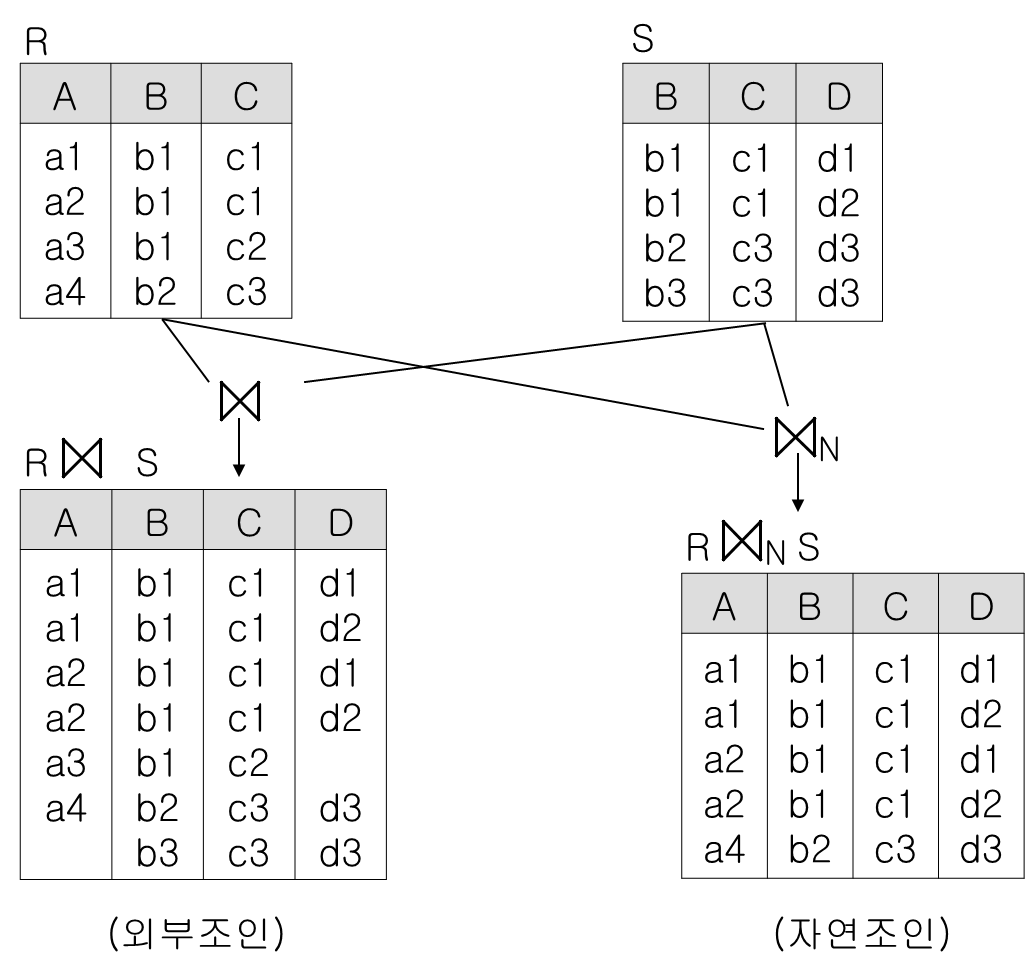
※ 외부 조인(OUTER JOIN : ▷◁+)
- 한 릴레이션에 있는 투플이 조인할 상대 릴레이션에 대응되는 투플이 없을 경우, 상대를 널(null) 투플로 만들어 결과 릴레이션에 포함
- 누락 정보를 처리하기 위한 조인의 확장
- 두 조인 릴레이션의 투플들 모두가 결과 릴레이션에 포함됨
예)
'데이터베이스' 카테고리의 다른 글
| [PL/SQL] 프로시저 (0) | 2023.03.13 |
|---|---|
| SQLD_데이터 모델링의 이해 (0) | 2022.09.20 |
| Tomcat다운로드&환경설정_HTML_국비_DAY40 (0) | 2022.04.26 |
| JDBC 실습_국비_DAY39 (1) | 2022.04.22 |
| DB 모듈화 (0) | 2022.04.22 |
